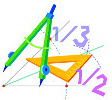
いきなり幾何の話を持出して不粋かも知れぬが,定規とコソパスとを有限回使って角を2等分することは簡単にできる.ただし,定規は点を結ぶ線分を引くか,これを左右に延長するかに限って使うことにする.また,コンパスは1点を中心に,ある半径の円を描くだけに使うことにする.

方法は先刻ご存知だろうが,念のために書くとつぎのとおりだ.まず,角の頂点ⓐを中心に適当な半径で円を描く
- つぎに,この円と両辺との交点ⓑを中心にそれぞれ再び円を描く
- あとの2円の交点ⓒと頂点とを結べば
- 角は見事に真二つになる.
では三等分
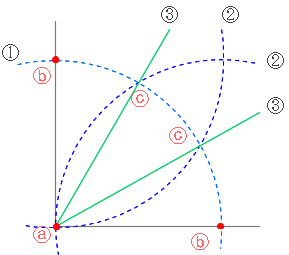
等分が成功するとつぎは3等分をやってみたくなるのが人情だ.
まず,直角をやってみる.
頂点ⓐを中心に円を描き
- 両辺との交点ⓑを中心に同じ半径で再び円を描く
- ここまでは2等分のときと同様だが,こんどはあとの2円どうしの交点でなく,はじめの円との交点ⓒ(2個できる)と頂点とをそれぞれ結ぶ
- めでたく直角は3等分できる.
解けないことが解けた
それなら,60度ではどうだろう.こんどはうまく行かぬ.柳の下にいつもどじょうとは限らない.「任意に与えられた角を3等分すること(ⅰ)」は「与えられた立方体の2倍の体積をもつ立方体を作図すること(ⅱ)」と「与えられた円と同じ面積の正方形を作図すること(ⅲ)」とともに,ソフィストの三大難問といわれ,ギリシャの昔から2000年間も解けなかった.
ところが,19世紀になり,はじじめの2問(ⅰ・ⅱ)はフランスの天才数学者ガロアの理論で解決された.また,最後の1問(ⅲ)も,1882年,リンデマソが解決した.ただし,どちらも「解けた」のではなく「解けない」ことが証明された.だから「角の3等分を作図せよ」といわれたら,頭のよい連中は手をつけようとしないはずだ.
そこを何とかする
けれども,そこを何とかとなったら,どうするか。戸川隼人氏はいう(数値計算入門,第2版,オーム社)。「頂点を中心に円を措く.角の約1/3と思われるところの円周上に印をつける.コンパスでその円弧の長さ(正確にいえば弦の長さ)を計り,その幅でもう2区間とってみる.要するに約1/3と思われる角度を3倍したわけである.それが運よくもとの角度に一致すればそれでおしまい.もし一致しなければ,余った角度についてまた同じことをやる.すなわち,その約1/3と思われる角度をとり,(前の幅に加えて*)コンパスを使ってそれを3倍し,それでも合わない部分をまた約3等分し・・‥‥,これをくり返せば余りの部分ほだんだん小さくなって,実用上は0とみなしてよいくらいになるであろう.」
ここで用いた手法,すなわち,だいたいの見当をつける,それを実際に試してみる,合わなかったら修正する,これを合うまでくり返すという方法は“逐次近似法”といって数値計算の基本的な考え方の一つだ.
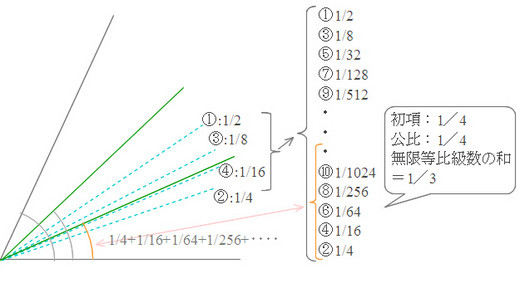
角の3等分方法を図示する.1/3は,二進法で0.01010101‥…・と表わせる.これは1/3=1/4+1/16+1/64+1/256+……だ.つまり,1/3は,初項が1/4で公比も1/4の無限等比級数の和になるわけだ.だから,まず角を2等分①し,その下半分をさらに2等分②する.できた四半分の上半分を再び2等分③し,その下半分をさらに2等分④する.これを何回もくり返せば,実用上角は3等分できるというわけだ.議論明快だし,半分の半分をくり返して3等分できるところが愉快だ.
最後の図の別図.こちらの方がわかりやすいかもしれない?
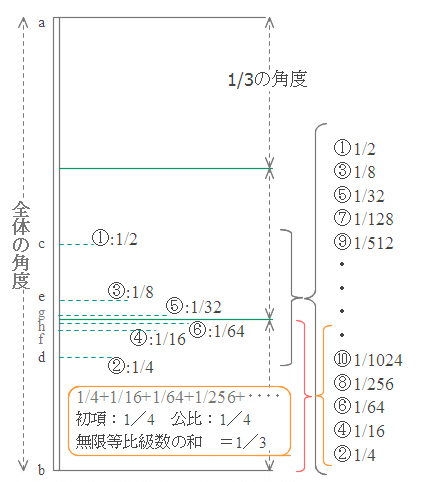
- まず角を2等分(c)
→ 角度は最初の1/2 - その下半分(c~b)を
さらに2等分(d)→ 同じく1/4 - できた四半分の上半分(c~d)を
再び2等分→ 同じく1/8 - その下半分(e~d)を
さらに2等分→ 同じく1/16 - これを何回も繰り返せば、実用上
角は3等分できる.
1/4+1/16+1/64+1/256・・・⇒1/3
* 初項:1/4 公比:1/4
無限等比級数の和となる
📖 参考書籍
数値計算入門,第2版,オーム社
戸川隼人
(いまや古本でしか入手できない?)
👀
古い古い一文です。
敬愛する味村重臣さんが、事務所のブログかクライアント先の教育誌に書いてくださった数あるものの一つを再編・再掲しました。
味村さんと切り離せない一つにコーヒーがあります。私も自宅で一人でもコーヒーをいれますが、味村さんもコーヒー好きで、お訪ねすると、まずコーヒをドリップしてくださいます。何回かのドリップタイムを挟みながら、延々とお話しをしたものです。味村宅を辞去するのが夕方になり、今頃の季節だと、帰り道134号湘南海岸道路で日没、運が良ければきれいな夕陽が見られたことを思い起こします。
最近は何事につけ、こういった[近似法]的な思考・手法が否定されたり、蔑ろにされているように感じます。デジタルだけでは生ききれない、昭和世代のひがみ・性でしょうか。
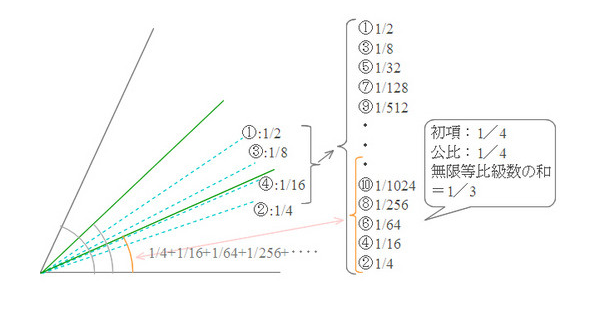

コメント