前回利用した標準化値は、検査データを性別年令別に、平均値を基準【100】として、その人の検査値が平均からどの程度に離れた(外れた)位置にあるかを示しています。逆に言えば、標準化値が【100】に近いほど、性別年令別に見た平均に近いことになります。
検査項目に拘わらず平均値を【100】としますので、検査項目の単位に関係なく見て比べることができます。
少し詳細に書くと、1標準偏差分(SD)を【10】とし平均の【100】に加減されますので、平均を挟み標準化値までにどの程度の仲間がいるかが分かります。
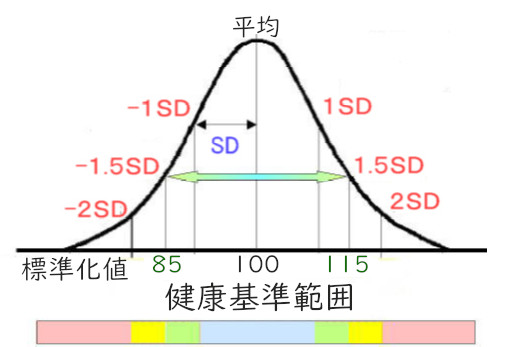
図のような平均値を中心に左右対称の釣り鐘型の分布 (正規分布) では、ご承知の通り、平均値と標準偏差(SD)及び度数の間に次の関係が成り立ちます。
- 80~120(100±2×標準偏差)の領域
95%の人が含まれます
この値より高い(低い)人は2.5%(100人中に2~3人)しかいません - 85~115(100±1.5×標準偏差)の領域
87%の人が含まれます
この値より高い(低い)人は6~7%(100人中に6~7人)います - 90~110(100±1×標準偏差)の領域
68%の人が含まれます
この値より高い(低い)人は16%(100人中に16人程度)います
👀
検査値を標準化値で表すことの大きなメリットは次の4つです。
- 性年令に応じた検査値のポジションを知ることができる
- 検査項目に共通の判断指標で分かりやすい
- 検査値やその変化が示す意味・重大さが理解し易い
- 検査項目を越えた比較ができる


コメント